Función a trozos es un nombre más general para una función que puede ser definida con la ayuda de múltiples funciones de correspondencia.
Una función f: X → Y es llamadauna función a trozos si puede ser definida con la ayuda de varias funciones lineales.
Podemos decir que tal función está definida en una serie de intervalos múltiples.
La notación general para definir una función a trozos es la siguiente,
Como se muestra en el ejemplo, punto y coma ócomas se utilizan al final de la columna.
Sin embargo, algunos los autores prefieren usar palabras como “si” o “para” en la columna derecha, y la palabra “ de lo contrario” también se puede utilizar para indicar el caso por defecto.
La gráfica de esta función también se divide en trozos, dependiendo del número de ecuaciones que se utilicen para definir la función.
Tal función es llamada de esta forma porque la definición de esta función cambia dependiendo del valor de la variable de entrada.
Aquí el uso de la palabra “a trozos” se hace para describir la propiedad de esa función, que es válida para una ecuación / pieza de la función pero no en todo el dominio de la función.
La función a trozos tiene una serie de funciones en su cuerpo, el dominio de cada una de ellas se define por separado. El gráfico del ejemplo dado previamente luciría de esta forma,
Es claro que el gráfico anterior contiene dos piezas separadas para indicar dos ecuaciones diferentes, por lo tanto representa la función como un todo.
Un caso especial de la función a trozos es la función piso que tiene un número infinito de piezas.
El valor absoluto de cualquier número es su distancia absoluta del cero, nunca es negativo dado que la distancia nunca es negativa.
A la luz de la afirmación anterior se puede decir que el valor absoluto de cualquier número es el número mismo hecho positivo.
La función de valor absoluto es generalmente una función par, ya que cualquier número y su equivalente negativo tienen los mismos valores absolutos.
Tal función es estrictamente decreciente en el intervalo (- ∞, 0] y estrictamente creciente en el intervalo [0, ∞).
El ejemplo ilustrado arriba es también una función de valor absoluto.
Todas las gráficas de las funciones de valor absoluto están en forma de letra “V”, ya seanrectas u oblicuas en función del valor de la variable.
Esto se debe a que un valor negativo en cada variable es igual en magnitud pero opuesto en su dirección.
Pero definitivamente no se puede llegar a la conclusión de que todas las funciones con forma de V son funciones de valor absoluto, esto es simplemente una probabilidad.
Graficar una función de valor absoluto es muy esencial para utilizar algunos valores negativos en la tabla T.
Esto se debe a que las funciones de valor absoluto se comportan algo diferente de otras funciones lineales.
Generalmente una función real de valor absoluto se comporta de forma continua en todos sus dominios.
También tal función sería diferenciable para todos los valores excepto el cero.
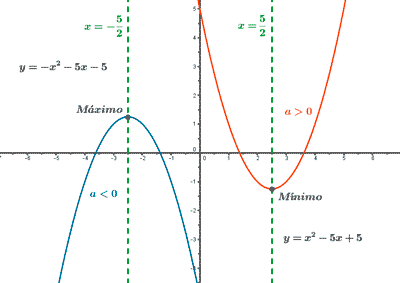
 entre las variables x e y:
entre las variables x e y: entre las variables x e y:
entre las variables x e y: