FUNCIONES ALGEBRAICAS
Si una función puede construirse usando operaciones algebraicas (como suma, resta, multiplicación y sacar raices) se le llama función alebraica. Cualquier función racional es una función algebraica.
FUNCION POLINOMIAL
Una función polinómica es aquella que está definida por un polinomio:
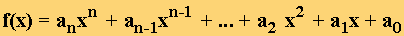

f(x)=2x4−x2+1x2−4


Una función polinómica es aquella que está definida por un polinomio:
donde a0, a1 ... an-1, an son números reales que se llaman coeficientes del polinomio y n es el grado del polinomio.
Las características generales de las funciones polinómicas son las siguientes:
1) El dominio de definición es el conjunto de los números reales (R).
2) Son siempre continuas.
3) No tienen asíntotas.
4) Cortan al eje X, como máximo, un número de veces igual que el grado del polinomio.
5) Cortan el eje Y en el punto (0, a0).
6) El número de máximos y mínimos relativos es, a lo sumo, igual al grado del polinomio menos uno.
7) El número de puntos de inflexión es, a lo sumo, igual al grado del polinomio menos dos.
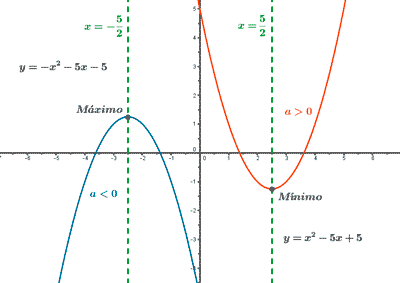
Funciones polinómicas de segundo grado: parábolas

Función racional
| Definición de función racional |
Una función racional
donde
|

Figura 4 - Función recíproca
Un ejemplo sencillo de una función racional es la función f(x)=1/x , cuyo dominio es {x≠0} ; esto es la función recíproca que se dibuja en la figura 4.La función
es una función racional con dominio \left{ x|x \neq \pm 2 \right}$. La figura 5 ilustra su gráfica.

Figura 5 - Función racional
Función radical
La función f(x)=x1/n=x√n es una función raíz. Para n=2 es la función raíz cuadrada f(x)=x√ , cuyo dominio es [0,∞ } y cuya gráfica es la mitad superior de la parábola x=y2 . Para otros valores pares de n , la grafica de y=x√n es similar a la de y=x√ . Para n=3 tenemos la función raíz cúbica f(x)=x√3 cuyo dominio es R (recuerde que todo número real tiene una raíz cúbica) y cuya gráfica se ilustra en la figura 6(b). La gráfica de y=x√n para n impar (n>3 ) es similar a la de y=x√3 .

No hay comentarios:
Publicar un comentario