Unidad 1 Números Reales
1.1.- La Recta Numérica
La recta numérica es un gráfico unidimensional de una línea recta en la que los números enteros son mostrados como puntos especialmente marcados que están separados uniformemente.
La recta numérica. Aunque la imagen de arriba muestra solamente los números enteros entre -9 y 9, la recta incluye todos los números reales, continuando «ilimitadamente» en cada sentido.
(http://es.wikipedia.org/wiki/Recta_num%C3%A9rica)
1.2.- Los Números Reales
Número real, cualquier número racional o irracional. Los números reales pueden expresarse en forma decimal mediante un número entero, un decimal exacto, un decimal periódico o un decimal con infinitas cifras no periódicas.
El conjunto de los números reales
Número Naturales (N): números con los que contamos (también se les llama enteros positivos.  )
)
Enteros (E): conjunto de todos los números naturales con sus opuestos (negativos) y el cero.  .
.
Racionales: conjunto formado por todos los números que se pueden escribir en la forma  , donde m y n son enteros
, donde m y n son enteros  .
.
Número Reales (R): todos los racionales y los irracionales. Los números racionales tienen representaciones decimales repetitivas (periódicas), en tanto que los irracionales tienen representaciones no repetitivas infinitas.
(http://www.eplc.umich.mx/salvadorgs/matematicas1/contenido/CapI/1_5_Numeros%20Reales.htm)
1.3.- Propiedades De Los Números Reales
Los números reales son los números que se utilizan para la medición de cantidades reales. Incluyen los números racionales, números irracionales, números enteros, decimales, etc. Estas cantidades reales incluyen longitud, velocidad, temperatura ambiente, tasas de crecimiento y muchos más. Los números racionales e irracionales llenan completamente la recta numérica y forman el conjunto de los números reales. En palabras más simples, los números reales se pueden clasificar en números racionales y números irracionales. Estos números racionales se pueden dividir en números enteros y fraccionnes
(http://mitecnologico.com/igestion/Main/PropiedadesDeLosNumerosReales)
1.4.- Intervalos Y su Representación Mediante Desigualdades
Una desigualdad es de una forma: 10 + 3 es mayor que 6. Se le representa por: Desigualdad: 10 + 3 > 6
Esta desigualdad se transforma en inecuación, cuando se introduce una incognita: Inecuacion: 10 + x > 6
En la recta numérica existe una relación de orden.
Cuando tenemos dos puntos de la recta numérica A y B, se pueden dar una de tres alternativas:
A es mayor que B A > B
A es igual a B A = B
A es menor que B A < B
Entonses por lo siguiente:
A > B v A=B
Destacamos que a < b es equivalente a b>a y así con otras expresiones, que se pueden “dar vuelta”.
Intervalos en los Reales (IR)
La Expresión: {x IR / a < x < b} se conoce como Intervalo, representa al conjunto de todos los números reales que
están entre otros dos reales “a” y “b” dados. En este caso x no puede ser ni “a” ni “b”.
están entre otros dos reales “a” y “b” dados. En este caso x no puede ser ni “a” ni “b”.
Tipos de Intervalos:
Intervalo Abierto: Conjunto de números entre a y b, sin incluirlos, se simboliza por: ( )
Intervalo Cerrado: Conjunto de números entre a y b, incluidos ambos. Se simboliza po: [ ]
Intervalo Semiabierto por Derecha: Intervalo de puntos entre a y b, que incluye a “a” pero excluye a “b”. Simboliza: [ )
Intervalo Semiabierto por Izquierda: ( ]
Representación GRAFICA de intervalos:
[-3,6] -3< x < 6
(4,9) 4 < x < 9
(1,+ ∞) 1 < x < + ∞
(https://sites.google.com/site/mago9292/unidad-1-numeros-reales/1-4---intervalos-y-su-representacion-mediante-desigualdades)
1.5.- Resolución de Desigualdad de Primer Grado con una Incógnita y de Desigualdad Cuadrática con una Incógnita
Desigualdades de primer grado con una incógnita
Las desigualdades de primer grado (lineales), se pueden resolver de una manera similar que las ecuaciones lineales.
Es decir, se puede despejar la incógnita utilizando operaciones idénticas en ambos lados de la desigualdad.
Como veremos en los ejemplos, es necesario tomar en cuenta una diferencia muy importante, pues cuando se multiplica una desigualdad por algún valor negativo, la dirección de la desigualdad se invierte, es decir, de menor que cambia a menor que y viceversa. Desigualdades de segundo grado con una incógnita Las desigualdades de primer grado (lineales), se pueden resolver de una manera similar que las ecuaciones lineales. De acuerdo a las características de la expresión cuadrática, podemos determinar si la resolveremos por fórmula general, por factorización, ó despejando. Además de tener en cuenta el efecto de la multiplicación por números negativos en la dirección de la desigualdad, también tenemos que considerar el efecto de la raiz cuadrada. Este efecto lo explicaremos en los ejemplos. El resultado lo representaremos en notación de intervalos y con representación sobre la recta númerica. Ejemplos Resolveremos un par de ejemplos de cada tipo de desigualdad. Comenzaremos con las de primer grado con una incógnita. 1) 3x – 5 ≥ 5x + 15 Sumamos 5 a los dos lados de la desigualdad 3x – 5 + 5 ≥ 5x + 15 + 5 3x ≥ 5x + 20 Restamos 5x en ambos lados 3x – 5x ≥ 5x + 20 – 5x -2x ≥ 20 Multiplicamos ambos lados por -1/2 * -1/2(-2x) ≤ -1/2(20) x ≤ -10 * La dirección de la desigualdad cambia al multiplicar por un número negativo. El resultado es el intervalo (-∞ , -10]
Las desigualdades de primer grado (lineales), se pueden resolver de una manera similar que las ecuaciones lineales.
Es decir, se puede despejar la incógnita utilizando operaciones idénticas en ambos lados de la desigualdad.
Como veremos en los ejemplos, es necesario tomar en cuenta una diferencia muy importante, pues cuando se multiplica una desigualdad por algún valor negativo, la dirección de la desigualdad se invierte, es decir, de menor que cambia a menor que y viceversa. Desigualdades de segundo grado con una incógnita Las desigualdades de primer grado (lineales), se pueden resolver de una manera similar que las ecuaciones lineales. De acuerdo a las características de la expresión cuadrática, podemos determinar si la resolveremos por fórmula general, por factorización, ó despejando. Además de tener en cuenta el efecto de la multiplicación por números negativos en la dirección de la desigualdad, también tenemos que considerar el efecto de la raiz cuadrada. Este efecto lo explicaremos en los ejemplos. El resultado lo representaremos en notación de intervalos y con representación sobre la recta númerica. Ejemplos Resolveremos un par de ejemplos de cada tipo de desigualdad. Comenzaremos con las de primer grado con una incógnita. 1) 3x – 5 ≥ 5x + 15 Sumamos 5 a los dos lados de la desigualdad 3x – 5 + 5 ≥ 5x + 15 + 5 3x ≥ 5x + 20 Restamos 5x en ambos lados 3x – 5x ≥ 5x + 20 – 5x -2x ≥ 20 Multiplicamos ambos lados por -1/2 * -1/2(-2x) ≤ -1/2(20) x ≤ -10 * La dirección de la desigualdad cambia al multiplicar por un número negativo. El resultado es el intervalo (-∞ , -10]
(http://asesoriasmfq.wordpress.com/cursos/calculo-diferencial/u1-numeros-reales/1-5-resolucion-de-desigualdades-de-primer-grado-con-una-incognita-y-de-desigualdades-cuadraticas-con-una-incognita/)
1.6.- Valor Absoluto y su Propiedades
En matemática, el valor absoluto o módulo1 de un número real es su valor numérico sin tener en cuenta su signo, sea este positivo (+) o negativo (-). Así, por ejemplo, 3 es el valor absoluto de 3 y de -3. El valor absoluto está relacionado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos. El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como son los cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.
(http://es.wikipedia.org/wiki/Valor_absoluto)
1.7.- Resolución de Desigualdades que Incluyan valor absoluto
El valor absoluto de un valor o expresión describe su distancia de 0, pero elimina información sobre el signo del número o la dirección. El valor absoluto es siempre positivo o cero, y un valor absoluto positivo pudo resultar de un valor original positivo o negativo.
Cuando se resuelven y grafican desigualdades de valores absolutos, tenemos que considerar el comportamiento del valor absoluto y las Propiedades de la Desigualdad. Este tipo de desigualdades se comportan de manera interesante — empecemos.
Valor Absoluto
Sabemos que el valor absoluto de un número es una medida de tamaño pero no de dirección. Por ejemplo, |27| y |-27| equivalen a 27 — el valor absoluto indica la distancia desde 0, pero no describe la dirección.
Si miramos el reporte del tiempo en las noticias, podríamos escuchar algo como: "Hoy, la temperatura máxima fue de 72°, pero tendremos una oscilación de 10° en la temperatura de mañana. Le daré más detalles después de estos mensajes." Basado en ésta información, la máxima de mañana podría ser de 62° u 82°. El hombre del tiempo ha dicho la diferencia entre temperaturas, pero no nos ha revelado en qué dirección cambiarán.
Encontrar el valor absoluto de números con signo puede ser muy fácil — sólo elimina cualquier signo negativo.
Considera |m| = 7.5. Sabemos el valor absoluto de m, pero el valor original pudo haber sido positivo o negativo. Por lo que en este caso decimos que m = 7.5 o -7.5. La gráfica de abajo muestra |m| = 7.5 en la recta numérica. Nota que hemos graficado las dos posibles soluciones.
(http://asesoriasmfq.wordpress.com/cursos/calculo-diferencial/u1-numeros-reales/1-7-resolucion-de-desigualdades-que-incluyan-valor-absoluto/)
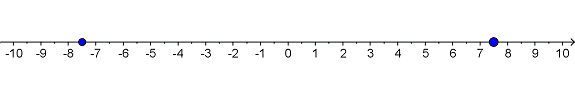









No hay comentarios:
Publicar un comentario